跳到主要内容

普里姆算法

提示
  1. 普里姆算法概念：一种贪婪算法，用于在加权图中找到包含所有顶点且总权重最小的边的子集，形成最小生成树。
  2. 工作原理：从单个顶点开始，逐步添加连接树与新顶点的最小边，直到包含所有顶点。
  3. 应用场景：普里姆算法适用于网络设计、电缆布线和制定网络协议等领域，时间复杂度为 O(E log V)。

Prim算法是一种最小生成树算法，它以图作为输入，并找出图的边的子集，这些边满足以下条件：

  • 形成包括每个顶点的树
  • 在所有可以从图中形成的树中具有最小权重之和

Prim算法的工作原理​

它属于一类称为贪婪算法的算法，它寻找局部最优解，以期找到全局最优解。

我们从一个顶点开始，不断添加权重最低的边，直到达到目标。

实现Prim算法的步骤如下：

  1. 使用随机选择的顶点初始化最小生成树。
  2. 查找连接树与新顶点的所有边，找到最小的边并将其添加到树中。
  3. 重复步骤2，直到获得最小生成树。

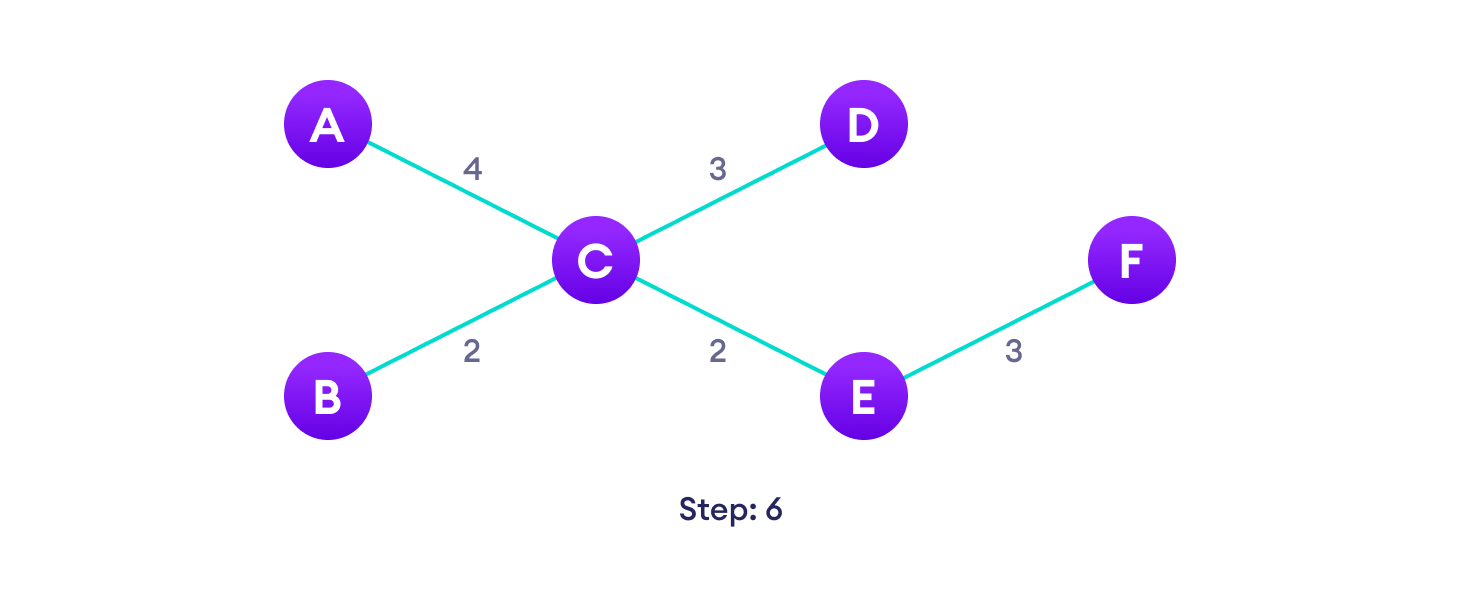
Prim算法示例​

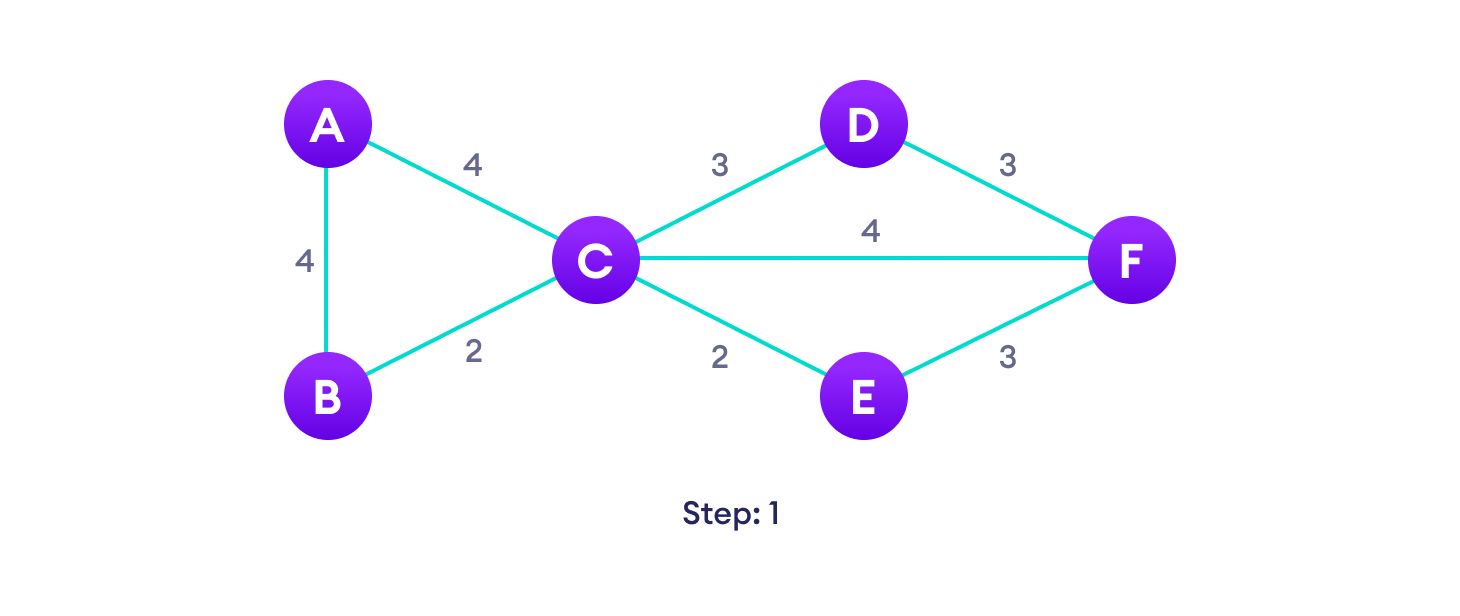
从加权图开始

选择一个顶点

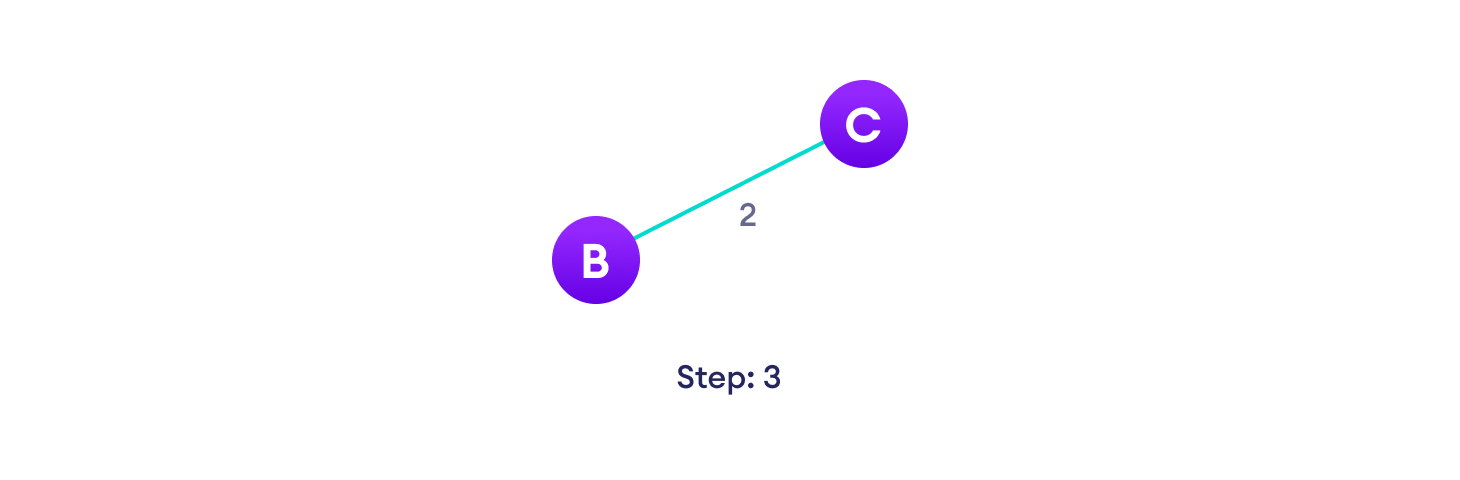
选择从该顶点开始的最短边并添加

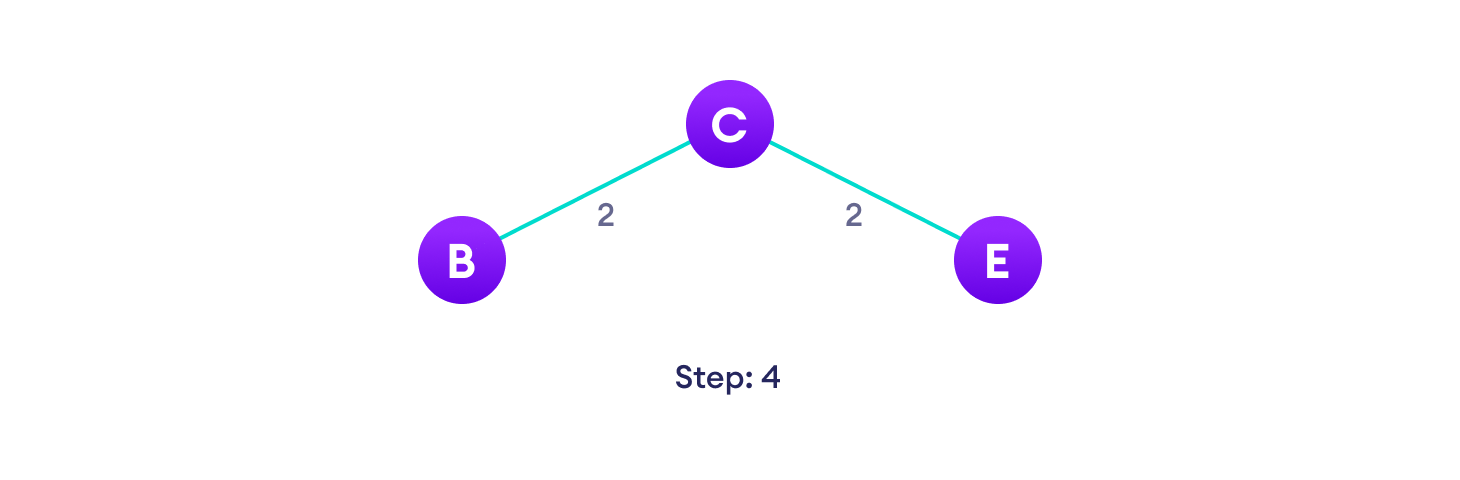
选择尚未包括在解决方案中的最近顶点

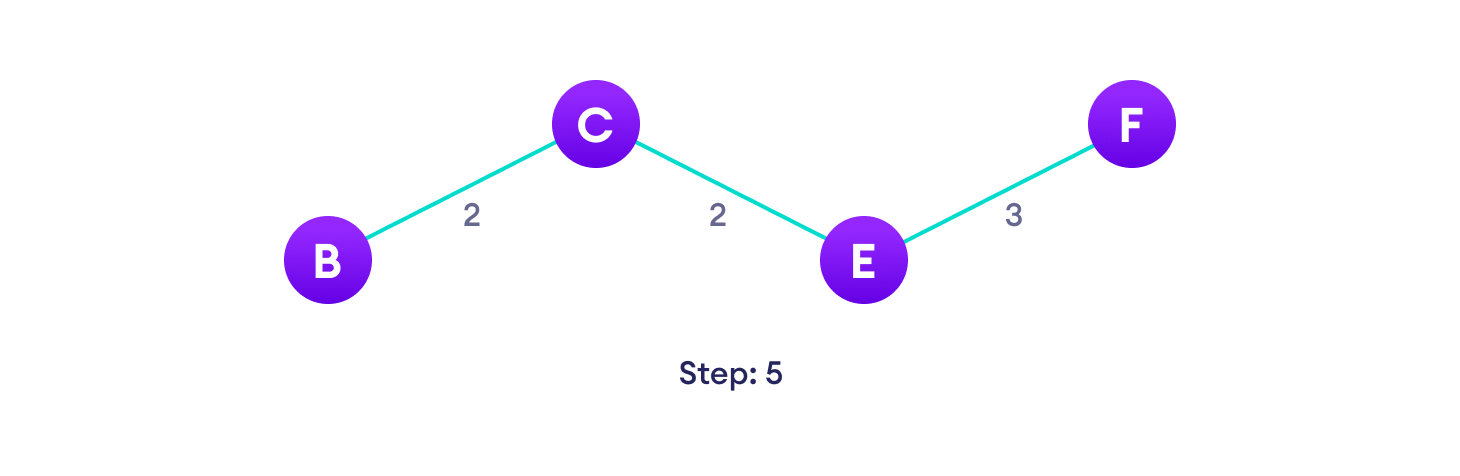
选择尚未包括在解决方案中的最近边，如果有多个选择，则随机选择一个

重复直到生成生成树

Prim算法伪代码​

Prim算法的伪代码显示了如何创建两个顶点集U和V-U。U包含已访问的顶点列表，而V-U包含尚未访问的顶点列表。我们逐个将顶点从集合V-U移动到集合U，方法是连接具有最小权重的边。

T = ∅;
U = { 1 };
while (U ≠ V)
    let (u, v) be the lowest cost edge such that u ∈ U and v ∈ V - U;
    T = T ∪ {(u, v)}
    U = U ∪ {v}

Python、Java和C/C++示例​

尽管使用图的邻接矩阵表示，但此算法也可以使用邻接表来提高其效率。

Python Java C C++

# Python中的Prim算法

INF = 9999999
# 图中的顶点数
V = 5
# 创建一个大小为5x5的二维数组
# 用于表示图的邻接矩阵
G = [[0, 9, 75, 0, 0],
     [9, 0, 95, 19, 42],
     [75, 95, 0, 51, 66],
     [0, 19, 51, 0, 31],
     [0, 42, 66, 31, 0]]
# 创建一个数组来跟踪选定的顶点
# 如果选定则为True，否则为False
selected = [0, 0, 0, 0, 0]
# 将边数设置为0
no_edge = 0
# 最小生成树中的边数将始终小于(V - 1)，其中V是图中的顶点数
# 选择第0个顶点并将其设置为True
selected[0] = True
# 打印边和权重
print("Edge : Weight\n")
while (no_edge < V - 1):
    # 对于集合S中的每个顶点，查找所有相邻顶点
    # 计算从步骤1中选择的顶点到它的距离。
    # 如果顶点已在集合S中，请将其丢弃，否则
    # 选择距离步骤1中选择的顶点最近的另一个顶点。
    minimum = INF
    x = 0
    y = 0
    for i in range(V):
        if selected[i]:
            for j in range(V):
                if ((not selected[j]) and G[i][j]):
                    # not in selected and there is an edge
                    if minimum > G[i][j]:
                        minimum = G[i][j]
                        x = i
                        y = j
    print(str(x) + "-" + str(y) + ":" + str(G[x][y]))
    selected[y] = True
    no_edge += 1

普里姆算法在 Java 和 C 中的实现​

// Java 中的普里姆算法

import java.util.Arrays;

class PGraph {

  public void Prim(int G[][], int V) {

    int INF = 9999999;

    int no_edge; // 边的数量

    // 创建一个数组跟踪选中的顶点
    // 选中的将变为 true，否则为 false
    boolean[] selected = new boolean[V];

    // 最初将 selected 设置为 false
    Arrays.fill(selected, false);

    // 将边的数量设置为 0
    no_edge = 0;

    // 最小生成树中的边数量总是小于 (V -1)，其中 V 是图中的顶点数

    // 选择第 0 个顶点并将其设置为 true
    selected[0] = true;

    // 打印边和权重
    System.out.println("Edge : Weight");

    while (no_edge < V - 1) {
      // 对于集合 S 中的每个顶点，找到所有相邻顶点
      // 计算从步骤 1 中选择的顶点到该顶点的距离。
      // 如果顶点已在集合 S 中，则舍弃它，否则
      // 选择另一个顶点，最接近步骤 1 中选择的顶点。

      int min = INF;
      int x = 0; // 行号
      int y = 0; // 列号

      for (int i = 0; i < V; i++) {
        if (selected[i] == true) {
          for (int j = 0; j < V; j++) {
            // 不在 selected 中并且存在边
            if (!selected[j] && G[i][j] != 0) {
              if (min > G[i][j]) {
                min = G[i][j];
                x = i;
                y = j;
              }
            }
          }
        }
      }
      System.out.println(x + " - " + y + " :  " + G[x][y]);
      selected[y] = true;
      no_edge++;
    }
  }

  public static void main(String[] args) {
    PGraph g = new PGraph();

    // 图中的顶点数
    int V = 5;

    // 创建一个 5x5 的二维数组
    // 作为邻接矩阵来表示图
    int[][] G = { { 0, 9, 75, 0, 0 }, { 9, 0, 95, 19, 42 }, { 75, 95, 0, 51, 66 }, { 0, 19, 51, 0, 31 },
        { 0, 42, 66, 31, 0 } };

    g.Prim(G, V);
  }
}
// C 中的普里姆算法

#include<stdio.h>
#include<stdbool.h>

#define INF 9999999

// 图中的顶点数
#define V 5

// 创建一个 5x5 的二维数组
// 作为邻接矩阵来表示图
int G[V][V] = {
  {0, 9, 75, 0, 0},
  {9, 0, 95, 19, 42},
  {75, 95, 0, 51, 66},
  {0, 19, 51, 0, 31},
  {0, 42, 66, 31, 0}};

int main() {
  int no_edge;  // 边的数量

  // 创建一个数组跟踪选中的顶点
  // 选中的将变为 true，否则为 false
  int selected[V];

  // 最初将 selected 设置为 false
  memset(selected, false, sizeof(selected));

  // 将边的数量设置为 0
  no_edge = 0;

  // 最小生成树中的边数量总是小于 (V -1)，其中 V 是图中的顶点数

  // 选择第 0 个顶点并将其设置为 true
  selected[0] = true;

  int x;  // 行号
  int y

;  // 列号

  // 打印边和权重
  printf("Edge : Weight\n");

  while (no_edge < V - 1) {
    // 对于集合 S 中的每个顶点，找到所有相邻顶点
    // 计算从步骤 1 中选择的顶点到该顶点的距离。
    // 如果顶点已在集合 S 中，则舍弃它，否则
    // 选择另一个顶点，最接近步骤 1 中选择的顶点。

    int min = INF;
    x = 0;
    y = 0;

    for (int i = 0; i < V; i++) {
      if (selected[i]) {
        for (int j = 0; j < V; j++) {
          if (!selected[j] && G[i][j]) {  // 不在 selected 中并且存在边
            if (min > G[i][j]) {
              min = G[i][j];
              x = i;
              y = j;
            }
          }
        }
      }
    }
    printf("%d - %d : %d\n", x, y, G[x][y]);
    selected[y] = true;
    no_edge++;
  }

  return 0;
}
// C++中的Prim算法

#include <cstring>
#include <iostream>
using namespace std;

#define INF 9999999

// 图中的顶点数
#define V 5

// 创建一个大小为5x5的二维数组
// 用于表示图的邻接矩阵

int G[V][V] = {
  {0, 9, 75, 0, 0},
  {9, 0, 95, 19, 42},
  {75, 95, 0, 51, 66},
  {0, 19, 51, 0, 31},
  {0, 42, 66, 31, 0}};

int main() {
  int no_edge;  // 边的数量

  // 创建一个数组来跟踪选定的顶点
  // 如果选定则为true，否则为false
  int selected[V];

  // 初始时将selected数组的所有元素设置为false
  memset(selected, false, sizeof(selected));

  // 将边的数量设置为0
  no_edge = 0;

  // 最小生成树中的边数始终小于(V -1)，其中V是图中的顶点数

  // 选择第0个顶点并将其设置为true
  selected[0] = true;

  int x;  // 行号
  int y;  // 列号

  // 打印边和权重
  cout << "边"
     << " : "
     << "权重";
  cout << endl;
  while (no_edge < V - 1) {
    // 对于集合S中的每个顶点，查找所有相邻顶点
    // 计算从步骤1中选择的顶点到它的距离。
    // 如果顶点已在集合S中，请将其丢弃，否则
    // 选择距离步骤1中选择的顶点最近的另一个顶点。

    int min = INF;
    x = 0;
    y = 0;

    for (int i = 0; i < V; i++) {
      if (selected[i]) {
        for (int j = 0; j < V; j++) {
          if (!selected[j] && G[i][j]) {  // 不在selected中并且有边相连
            if (min > G[i][j]) {
              min = G[i][j];
              x = i;
              y = j;
            }
          }
        }
      }
    }
    cout << x << " - " << y << " :  " << G[x][y];
    cout << endl;
    selected[y] = true;
    no_edge++;
  }

  return 0;
}

Prim算法与Kruskal算法的对比​

Kruskal算法是另一种流行的最小生成树算法，它使用不同的逻辑来查找图的最小生成树（MST）。Kruskal算法不是从一个顶点开始，而是将所有边按权重从低到高排序，然后逐渐添加最小的边，忽略那些会创建循环的边。

Prim算法复杂性​

Prim算法的时间复杂度是 O(E log V)。

Prim算法的应用​

  • 布置电线电缆
  • 网络设计
  • 制定网络周期的协议
最后于 更新