跳到主要内容

弗洛伊德-沃舍尔算法

提示
  1. 算法定义：弗洛伊德-沃舍尔算法用于计算加权图中所有顶点对之间的最短路径，适用于有向和无向图，但不适用于含有负权重循环的图。
  2. 工作原理：算法通过创建和更新一个矩阵来逐步计算每对顶点之间的最短距离，利用动态规划的方法实现。
  3. 应用场景：该算法广泛用于寻找有向图的最短路径，计算有向图的传递闭包，求解实数矩阵的逆矩阵，以及测试无向图是否为二分图等。

Floyd-Warshall Floyd-Warshall 算法是一种用于找出加权图中所有顶点对之间最短路径的算法。该算法适用于有向和无向加权图。但是，它不适用于含有负权重循环的图（即循环中边的权重和为负）。

加权图是每条边都有数值权重的图。

Floyd-Warshall 算法也被称为弗洛伊德算法、罗伊-弗洛伊德算法、罗伊-沃舍尔算法或者 WFI 算法。

这个算法遵循动态规划方法来找到最短路径。

Floyd-Warshall 算法是如何工作的？​

假设给定图为：

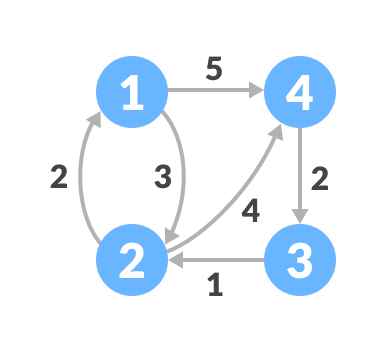
graph

按照以下步骤找出所有顶点对之间的最短路径。

  1. 创建一个维度为 n*n 的矩阵 A0，其中 n 是顶点的数量。行和列分别以 i 和 j 索引。i 和 j 是图的顶点。

    每个单元格 A[i][j] 填充从 第 i 个 顶点到 第 j 个 顶点的距离。如果 第 i 个 顶点到 第 j 个 顶点没有路径，则单元格保留为无穷大。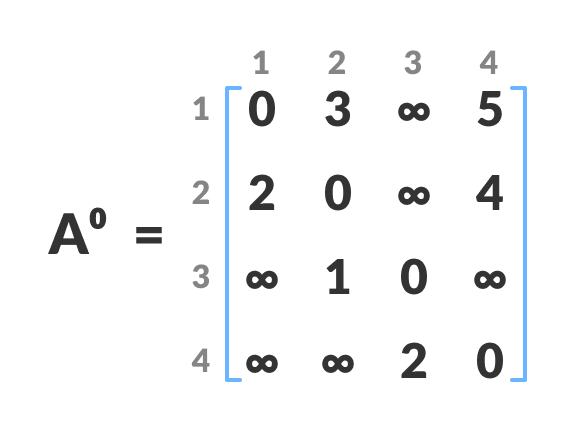

    matrix floyd warshall algorithm

  2. 现在，使用矩阵 A0 创建矩阵 A1。第一列和第一行的元素保持不变。其余单元格按以下方式填充。

    设 k 为源到目的地最短路径中的中间顶点。在此步骤中，k 是第一个顶点。A[i][j] 用 (A[i][k] + A[k][j]) 填充，如果 (A[i][j] > A[i][k] + A[k][j])。

    即，如果从源点到目的地的直接距离大于通过顶点 k 的路径，则该单元格填充为 A[i][k] + A[k][j]。

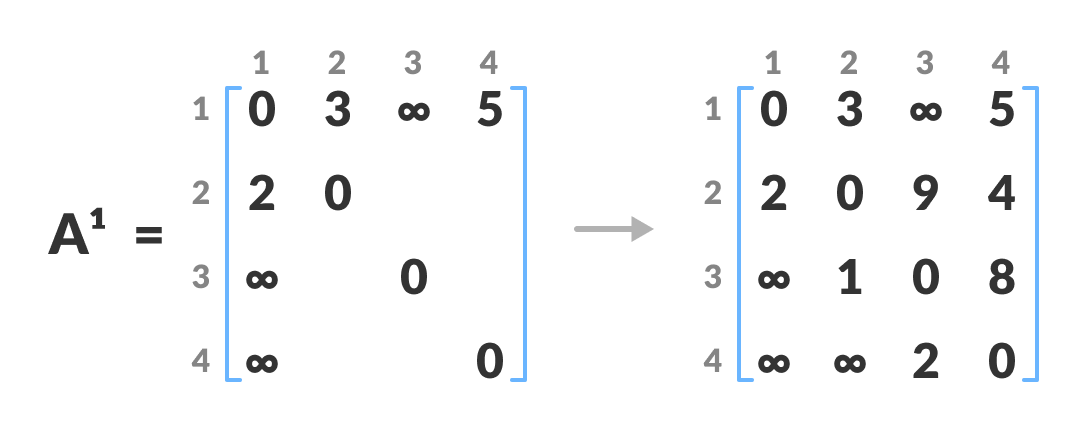
    在此步骤中，k 是顶点 1。我们计算通过此顶点 k 从源顶点到目的顶点的距离。 matrix floyd warshall algorithm

    例如：对于 A1[2, 4]，顶点 2 到 4 的直接距离是 4，通过顶点（即从顶点 2 到 1 和从顶点 1 到 4）的距离之和是 7。由于 4 < 7，A0[2, 4] 被填充为 4。

  3. 类似地，使用 A1 创建 A2。第二列和第二行的元素保持不变。

    在此步骤中，k 是第二个顶点（即顶点 2）。其余步骤与 步骤 2 相同。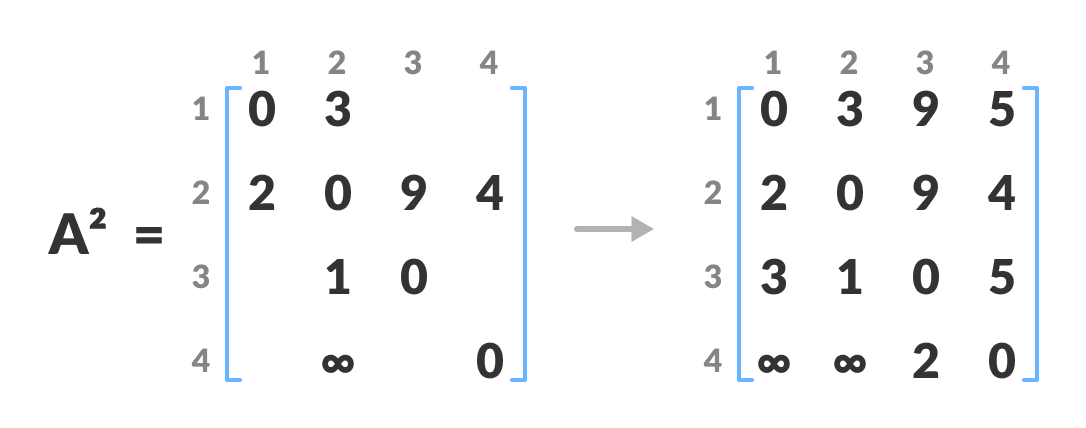 matrix floyd warshall algorithm

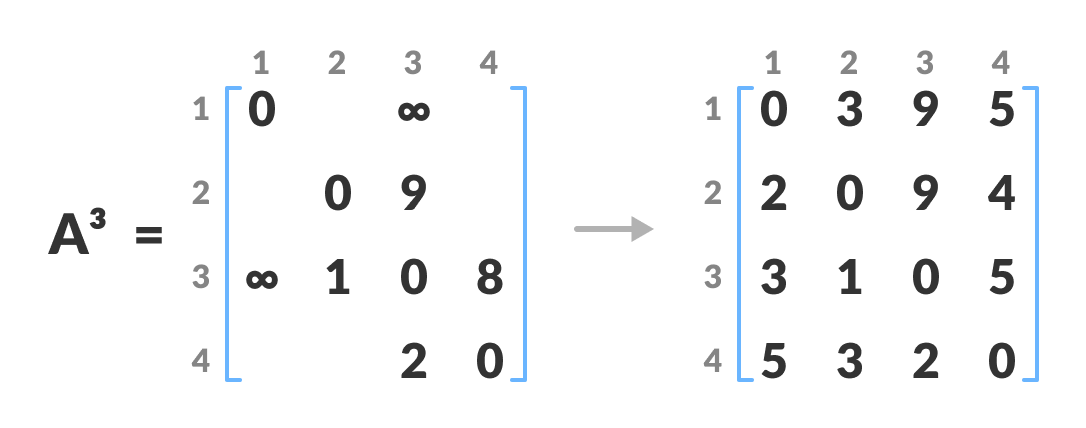
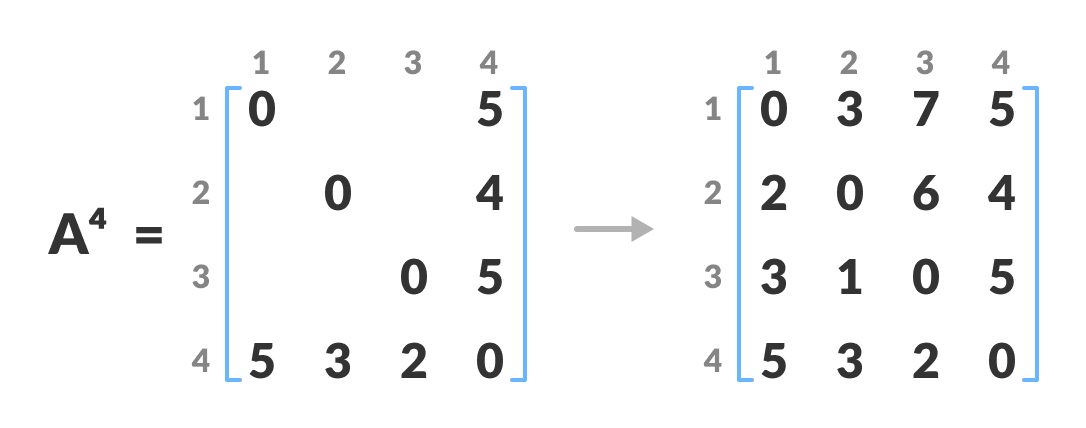
  4. 类似地，也创建 A3 和 A4。 matrix floyd warshall algorithm

     

    matrix floyd warshall algorithm

  5. A4 给出了每对顶点之间的最短路径。

Floyd-Warshall 算法​

n = no of vertices
A = matrix of dimension n*n
for k = 1 to n
    for i = 1 to n
        for j = 1 to n
            Ak[i, j] = min (Ak-1[i, j], Ak-1[i, k] + Ak-1[k, j])
return A

Python、Java 和 C/C++ 示例​

Python Java C C++

# Python 中的 Floyd Warshall 算法


# 顶点数
nV = 4

INF = 999


# 算法实现
def floyd_warshall(G):
    distance = list(map(lambda i: list(map(lambda j: j, i)), G))

    # 分别添加顶点
    for k in range(nV):
        for i in range(nV):
            for j in range(nV):
                distance[i][j] = min(distance[i][j], distance[i][k] + distance[k][j])
    print_solution(distance)


# 打印解决方案
def print_solution(distance):
    for i in range(nV):
        for j in range(nV):
            if(distance[i][j] == INF):
                print("INF", end=" ")
            else:
                print(distance[i][j], end="  ")
        print(" ")

G = [[0, 3, INF, 5],
     [2, 0, INF, 4],
     [INF, 1, 0, INF],
     [INF, INF, 2, 0]]
floyd_warshall(G)
// Java中的Floyd Warshall算法

class FloydWarshall {
  final static int INF = 9999, nV = 4;

  // 实现Floyd Warshall算法
  void floydWarshall(int graph[][]) {
    int matrix[][] = new int[nV][nV];
    int i, j, k;

    for (i = 0; i < nV; i++)
      for (j = 0; j < nV; j++)
        matrix[i][j] = graph[i][j];

    // 逐个添加顶点
    for (k = 0; k < nV; k++) {
      for (i = 0; i < nV; i++) {
        for (j = 0; j < nV; j++) {
          if (matrix[i][k] + matrix[k][j] < matrix[i][j])
            matrix[i][j] = matrix[i][k] + matrix[k][j];
        }
      }
    }
    printMatrix(matrix);
  }

  void printMatrix(int matrix[][]) {
    for (int i = 0; i < nV; ++i) {
      for (int j = 0; j < nV; ++j) {
        if (matrix[i][j] == INF)
          System.out.print("INF ");
        else
          System.out.print(matrix[i][j] + "  ");
      }
      System.out.println();
    }
  }

  public static void main(String[] args) {
    int graph[][] = { { 0, 3, INF, 5 }, { 2, 0, INF, 4 }, { INF, 1, 0, INF }, { INF, INF, 2, 0 } };
    FloydWarshall a = new FloydWarshall();
    a.floydWarshall(graph);
  }
}
// C语言中的Floyd-Warshall算法

#include <stdio.h>

// 定义顶点的数量
#define nV 4

#define INF 999

void printMatrix(int matrix[][nV]);

// 实现Floyd-Warshall算法
void floydWarshall(int graph[][nV]) {
  int matrix[nV][nV], i, j, k;

  for (i = 0; i < nV; i++)
    for (j = 0; j < nV; j++)
      matrix[i][j] = graph[i][j];

  // 逐个添加顶点
  for (k = 0; k < nV; k++) {
    for (i = 0; i < nV; i++) {
      for (j = 0; j < nV; j++) {
        if (matrix[i][k] + matrix[k][j] < matrix[i][j])
          matrix[i][j] = matrix[i][k] + matrix[k][j];
      }
    }
  }
  printMatrix(matrix);
}

void printMatrix(int matrix[][nV]) {
  for (int i = 0; i < nV; i++) {
    for (int j = 0; j < nV; j++) {
      if (matrix[i][j] == INF)
        printf("%4s", "INF");
      else
        printf("%4d", matrix[i][j]);
    }
    printf("\n");
  }
}

int main() {
  int graph[nV][nV] = {{0, 3, INF, 5},
             {2, 0, INF, 4},
             {INF, 1, 0, INF},
             {INF, INF, 2, 0}};
  floydWarshall(graph);
}
// C++中的Floyd-Warshall算法

#include <iostream>
using namespace std;

// 定义顶点的数量
#define nV 4

#define INF 999

void printMatrix(int matrix[][nV]);

// 实现Floyd-Warshall算法
void floydWarshall(int graph[][nV]) {
  int matrix[nV][nV], i, j, k;

  for (i = 0; i < nV; i++)
    for (j = 0; j < nV; j++)
      matrix[i][j] = graph[i][j];

  // 逐个添加顶点
  for (k = 0; k < nV; k++) {
    for (i = 0; i < nV; i++) {
      for (j = 0; j < nV; j++) {
        if (matrix[i][k] + matrix[k][j] < matrix[i][j])
          matrix[i][j] = matrix[i][k] + matrix[k][j];
      }
    }
  }
  printMatrix(matrix);
}

void printMatrix(int matrix[][nV]) {
  for (int i = 0; i < nV; i++) {
    for (int j = 0; j < nV; j++) {
      if (matrix[i][j] == INF)
        printf("%4s", "INF");
      else
        printf("%4d", matrix[i][j]);
    }
    printf("\n");
  }
}

int main() {
  int graph[nV][nV] = {{0, 3, INF, 5},
             {2, 0, INF, 4},
             {INF, 1, 0, INF},
             {INF, INF, 2, 0}};
  floydWarshall(graph);
}

Floyd Warshall算法复杂度​

时间复杂度​

这里有三个循环。每个循环具有常数复杂度。因此，Floyd-Warshall算法的时间复杂度为O(n3)。

空间复杂度​

Floyd-Warshall算法的空间复杂度为O(n2)。

Floyd Warshall算法的应用​

  • 用于查找有向图的最短路径
  • 用于查找有向图的传递闭包
  • 用于求解实数矩阵的逆矩阵
  • 用于测试无向图是否为二分图
最后于 更新